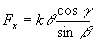Reverse engineering the bow - I

Reverse engineering the bow: a simple static model

Copyright by Ugo Bardi – 2000 (revised Aug 2001)

This text uses a simple model, known sometimes as the Hickman model, to calculate the relation of force vs. elongation (draw length) in bows. This relation is a fundamentalone for the performance and the ease of shooting of a bow. The calculations reported here are not meant to provide one with quantitative data, but just to build up simple models to understanding how the elastic machine we call "bow" works. We find that all bows (not including compounds) tend to have a nearly linear relation of force vs. draw length. "Recurving" the bow changes this characteristc in a favorable way which allows the bow to store more energy for the same final draw force.

In the design of a bow, one of the most important characteristics to be controlled is the relation of force versus draw length. This relation controls the amount of energy which can be transmitted to the arrow and the possibility of smooth handling of the bow. Modern compound bows optimize this relation by a complex system of pulleys which ensure a minimum force at the maximum draw. We would like all bows to behave as compound bows, but this is not possible. The best we can do for "non-compound" or traditional bows is to have a linear or nearly linear relation of force and elongation in such a way to avoid the sudden rise in force at high draws, something which is called "stack". When a bow goes "in stack" it becomes difficult to control and it even risks to break. Clearly nobody wants that, but some stacking may be unavoidable for short bows, as – for instance – for replicas of Indian or Turkish bows.

The shape of the Force vs. draw length relation also determines the elastic energy that can be stored in a bow. This energy can be seen graphically as the area under the curve. Again, compound bows maximize this energy, whereas the curve of a short bow is the most unfavorable one. These facts are rather well known in archery, but the exact reasons for bows to behave the way they do are not so clear. It appears that bows manufactured today, as well as ancient ones, have been optimized by trial and error to arrive to shapes and dimensions which are optimal or nearly optimal for the specific purposes for which they are (or were) built. There remains the question of understanding why exactly some combinations of parameters are better than others, something that we may classify as "reverse engineering the bow". This is the question that we will be trying to solve here. In another paper, we will examine the reverse engineering of the dynamic characteritics of the bow, here we'll consider only the "static" part.

The mathematical description of the behavior of a cantilever bar under an applied force is a very complex matter. For small deformations, however, the theory ends up with some simple formulas. In this case the deformation turns out to be simply proportional to the applied force. The deformation is also inversely proportional to the Young modulus (or stiffness) and is mediated by such factors as the cross sectional area of the beam and its momentum of inertia. In the case of bows, it is hard to think that we may consider the deformation to be "small", so in practice it is impossible to come out with a formula that would give us the Force vs. elongation characteristics for the whole range of deformation. However, it is not impossible to approximate the behavior of the bow as if it would be if it obeyed a simple linear relation, and here I would like to do just that.

The idea of modeling a bow in this way was developed already in the 30s by Hickman, so we can use what we can call the "Hickman model", shown in the figure below. Actually, the Hickman model describes an actual device, the torsion catapult widely used in classic times.

We shall assume from now on that a rigid arm connected to a cylindrical elastic element reasonably approximates the behavior of the flexible arm of a conventional bow. This said, the mathematical model is reasonably easy to construct. We start from a simple case assuming that the riser (the rigid part of the bow, where it is handled) has zero length. Here are the main parameters involved.

F: force at the arm tip, assumed proportional to the angle (it may be non zero at =0)
Fx: force parallel to the x axis "drawing force"
X draw of the bow (length from the arrow notch to the arrow rest, note that there is an Xo due to the stringing of the bow, so the effective length is X-Xo
La : length of the bow arm (the bow is assumed to be symmetrical, we consider only half of it

Lb Length of bow string (half of it, obviously)
The meaning of the angle symbols is self-explanatory

Now, as we see from the figure, there exist an elastic force on the tip of the bow. In order for the system to be in equilibrium the force of the archer’s pull transmitted through the string at the same point must match it exactly. The component of the force parallel to the bow arm has no effect since we assume the arm to be completely rigid.

Now, the force Fs, is simply obtained by the combination of the X and Y components (the Y component of the force comes from the other side of the bow, not considered here)

So , the equation we have at this point is:

It is now a question of finding a relation among  , and. This takes some work for the general, "strung" bow and we start first with the simplest case, that of a bow which is not strung at all, that is it has a zero bracing height.
Simple "zero bracing height" bow
In this case we have that = 2 and  = 90 – ;. It follows that:

Plotting Fx as a function of is not so greatly interesting, we rather want to plot it as a function of the elongation, X. Still in the simple case of the "unstrung" bow, (Lb=Ls) we have that

It is possible, but not so practical, to express Fx as an analytical function of x, but we can easily plot the two parameters for stepping values of . We assume both k and L = 1. We’ll also limit the X range to a value typical of most bows, that is we assume that the ratio of bow length to draw length is 2.5. This plot is obtained in this case for = 23 degrees.


We see that in these conditions the F vs. X relation is approximately linear. But no real bow is used unstrung, so this is just a test to see what our model can do.
Braced and recurved bows.
We want now to work with a more realistic model, one that starts "braced", as all bows do. In this case, the calculation is not so simple, but it can be done with a bit of work. We start from the equation we had found at the beginning:

From here on the problem is to express and  as a function of . We have that



 

from the above:

And finally:

In this expression F is shown as as a function of , but easily transformed as a function of since it is = 90 –, just change sines into cosines and the reverse
As before, we can now find an expression for X as a function of (or ). Here we must not forget that the elongation is measured starting from an Xo which it the distance of the notch point from the arrow rest point.


As before, we can plot F vs X by stepping the values of (or of). Here are the results for the same "realistic" values of the bow and stringing from zero to 20 degrees in steps of 4 degrees.

We see that increasing pre-stresses make the F vs. X relation non-linear. We can compare this result with the experimental data. This result agrees very well with the data for real bows, which do show a somewhat "concave" F vs X curve.


It is also clear that bracing the bow has reduced the amount of energy that can be stored in the bow in comparison to an unstrung bow. So why would anyone want to do it? This is a very complex matter and something that cannot be explained by a static calculation but requires a dynamic model of the shooting action. Let’s just say here that bracing the bow does reduce the energy available but makes the bow more efficient in transferring it to the arrow. In practice there is a trade-off of energy available and efficiency and the optimal degree of stringing is normally found by trial and error.
We can also play with the model to see what is the effect of "reversing" the bow, to make what is normally called a "recurved" bow as opposed to a straight or "long" bow. In an unbraced recurved bows the arms are bent in the opposite direction as that of the string. For the model we assume that the elastic force is not equal to zero for =0, but to a certain "residual" value. That is F = k( +o), with o the angle (negative) at which the bow arm is at rest. We can make a calculation for progressively higher values of this residual and the results are shown in the figure here. Here the stringing angle is 5 degrees and the "recurving" angle goes from zero to 20 degrees in steps of 4 degrees. Notice that the force is normalized, for increasing recurved bows we have to lower the leastic consatnt of the bow (k) in order to arrive to the same final value of F. It is a well know fact that the arms recurve bows must be more pliant than those of longbows for the same final force. We see anyway that the effect of recurving the bow is to substantially increase the amount of energy stored. This is what makes recurved bows superior to simple "straight" bows.

Finally, we can use the model to see what is the effect of a large elongation. Here are the results of a calculation with the same parameters as the previous one but where the bow arms are supposed to be pulled all the way to an angle of 60 degrees (which would be impossible in a real bow, the arms would break much before reaching that value)

Here, the model does not pretend to be a simulation of anything like a real bow since the mechanisms of deformation are much different for a cantilever bar (the case of a real bow) and for a rigid bar/torsion spring as we are considering here. Nevertheless we see that the results obtained seem to fit with reality, with the system noticeably going "stack" for x larger than about 1. Remembering that we have so far assumed the length of the arm to be unity, it means that the system can maintain a reasonable linear character for arrow of about ½ length as that of the bow, which makes sense if compared with the data for real bows. For even larger values of and correspondingly larger draw length, the curve becomes even more steep, as expected.
Risers.
The models described above are not very difficult to modify in order to take into account the presence of a rigid riser that holds the two flexible arms. However, the formulas become somewhat complex, so the results of the calculations are not reported here. It will suffice to say that – as easily imagined – a riser has a negative effect in forcing the arms to deform more than they would if the riser was not there. A bow with a rigid riser goes in stack for smaller deformations than a bow without a riser. Nevertheless, some kind of riser is necessary to get a firm hold of the bow and to provide a stable base for such things as stabilizers, sights, etc. Obviously, it should be as short as possible. It may be possible, however, that shortening the arms some gain in stability is obtained because of less vibration, again something that cannot be discussed within a static model
Conclusion:
The very simple model considered here (Hickman's model) can explain most of the characteristics of modern and ancient bows. In particular we have been able to "deconstruct" the bow parameters and to arrive to some conclusions as:

1. Bows are built with limited elongations (draw) to avoid a region for X/L (draw/bow length) larger than about 0.5 where the bow goes "in stack", that is the force starts rising up rapidly. Obviously, real bows may break even before reaching this region which is considered dangerous by all bow makers.
2. In the region of X/L<0.4 the F vs draw characteristic curve of the bow is nearly linear "by nature", no special trick of the bow-maker is necessary to obtain it. Different values of the bracing height affect very little this characteristic.
3. Bracing the bow reduces the amount of energy that can be stored as elastic energy of the arms, and as consequence the amount that can be transferred – in principle – to the arrow. Bracing has therefore a negative effect on this point. It is nevertheless absolutely necessary in bows since it affects the efficiency with which the energy can actually be transferred to the arrow
4. "Recurving" the bow, that is giving a negative curvature to the arms is the most important static factor that affects the bow performance in increasing the amount of storable energy and giving rise to a slow-rising characteristic curve which makes the bow smoother to handle. A good bow should be as recurved as possible, but there are of course limits to this in reason of the limited resistance of materials
5. Risers affect the force vs. elongation curve in an unfavorable way and should be made as short as possible

---